El ciclo Otto teórico es el ciclo ideal del motor Otto. El motor Otto también se conoce como motor de encendido por chispa debido a que la ignición del combustible se realiza a través de una chispa provocada por una bujía.También se conoce como motor de gasolina por el tipo de combustible que utiliza.
Una forma de estudiar el rendimiento de este motor es analizando su ciclo teórico. El ciclo teórico es una aproximación al ciclo real cn muchas simplificaciones. A la práctica, aparecen tantas variables que afectan al rendimiento del motor que calcular el ciclo real es prácticamente imposible. De todos modos el cico Otto teórico es una buena aproximación al ciclo real.
¿Cómo es el ciclo Otto de 4 tiempos?
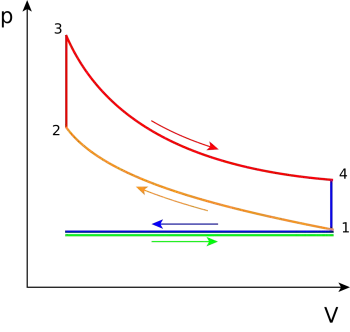
Los siguientes diagramas representan el ciclo Otto en un motor de 4 tiempos tanto en coordenadas P-V como en coordenadas T-S.
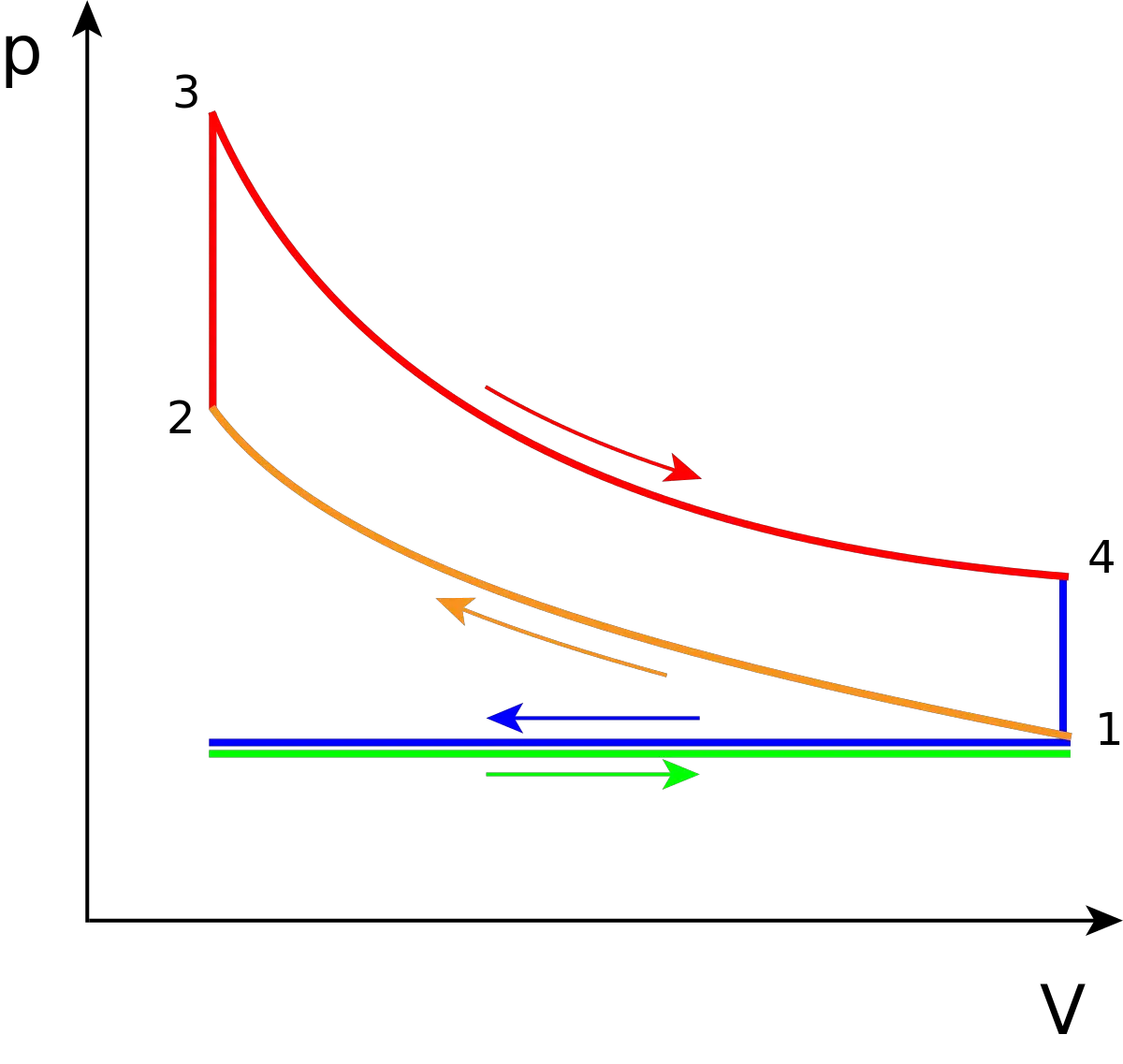
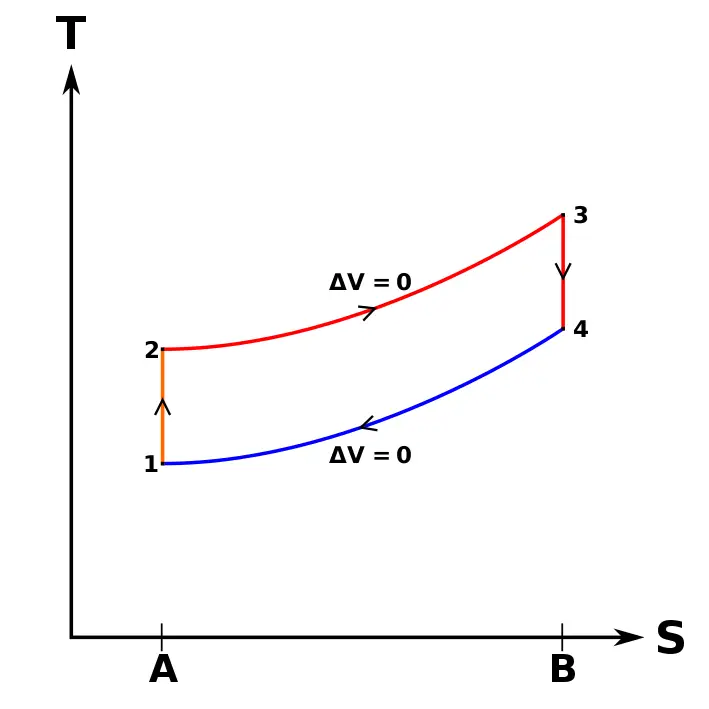
Las transformaciones termodinámicas que se verifican durante el ciclo Otto son:
- 1-2. Transformación adiabática i isentropica (sin intercambio de calor con el exterior). Compresión del fluido activo y correspondiente al trabajo L1 realizado por el pistón.
- 2-3. Transformación a volumen constante. Introducción instantánea del calor suministrado Q1.
- 3-4. Transformación adiabática. Expansión a presión constante y correspondiente trabajo L2 producido por el fluido activo.
- 4-1. Transformación a volumen constante. Sustracción instantánea del calor Q2.
En realidad, en el motor de 4 tiempos, la sustracción del calor se verifica durante la carrera de escape 1-0, y el fluido se introduce en el motor en la carrera de aspiración 0-1, lo cual se representa gráficamente en el diagrama P-V mediante una línea horizontal, mientras que en el diagrama T-S no es posible representarlo. Los efectos de ambos procesos se anulan mutuamente, sin ganancia ni pérdida de trabajo, razón por la cual no suelen considerarse en los diagramas ideales en coordenadas P-V las carreras de aspiración y escape, y el ciclo Otto está representado como un ciclo cerrado, en el cual el fluido activo vuelve a su estado inicial cuando llega a su término la fase de expulsión del calor 4-1.
¿Cómo es el ciclo Otto de 2 tiempos?
El ciclo Otto cambia ligeramente en un motor de 2 tiempos respecto al motor de 4 tiempos.
Primer tiempo - Amdisión compresión
Cuando el pistón del motor alternativo alcanza el PMI (Punto Muerto Inferior) empieza a desplazarse hasta el PMS (Punto Muerto Superior). Durante el recorrido el pistón crea una diferencia de presión que aspira la mezcla de aire y gasolina por la lumbrera de admisión hacia el cárter de precompresión. El combustible entra en forma gaseosa.
Cuando el pistón tapa la lumbrera, deja de entrar mezcla. Durante el resto del recorrido descendente, el pistón la comprime la mezcla en el cárter inferior, hasta que se descubre la lumbrera de transferencia que lo comunica con la cámara de compresión. Al comunicarse con la cámara de compresión la mezcla fresca precomprimida ayuda a expulsar los gases quemados del escape.
Cuando el pistón empieza a subir la lumbrera de transferencia permanece abierta una parte de la carrera y el cárter no coge aire fresco sino que retornan parte de los gases, perdiendo eficiencia de bombeo.A altas revoluciones se utiliza la inercia de la masa de los gases para minimizar este efecto. Es lo que se le llama renovación de la carga.
Segundo tiempo. Expansión y escape de gases
Una vez que el pistón del motor térmico ha alcanzado el PMS y la mezcla de aire y gasolina está comprimida, se la enciende por una chispa entre los dos electrodos de la bujía. Con el encendido el combustible libera energía y alcanza altas presiones y temperaturas en el cilindro. El pistón se desplaza hacia abajo, realizando trabajo hasta que se descubre la lumbrera de escape. Al estar a altas presiones, los gases quemados salen por ese orificio.
Características del ciclo Otto de 2 tiempos
El rendimiento de este motor es inferior respecto al motor de 4 tiempos, ya que tiene un rendimiento volumétrico menor y el escape de gases es menos eficaz. Los ciclos de 2 tiempos son más contaminantes. A nivel de potencia, el ciclo Otto de 2 tiempos ofrece un par motor en la unidad de tiempo más elevado para la misma cilindrada. Esta diferencia en el par motor se debe a que el motor de 2 tiempos hace una explosión en cada revolución, mientras el motor de 4 tiempos hace una explosión por cada 2 revoluciones, y cuenta con más partes móviles.
Éste tipo de motores se utilizan mayoritariamente en motores de poca cilindrada (ciclomotores, desbrozadoras, cortasetos, motosierras, etc), ya que es más barato y sencillo de construir, y su emisión de contaminantes elevada es muy baja en valor absoluto.
¿Cuál es el rendimiento del ciclo Otto?
Como el calor Q1 se introduce a volumen constante, el trabajo L2-3 realizado durante esa transformación es nulo, y la ecuación de conservación de la energía del fluido sin flujo se transforma en:
![]()
Como se trata de un ciclo ideal y, por tanto, el fluido operante es un gas perfecto, la variación de la energía interna durante su transformación a volumen constante vale:
![]()
De donde resulta:
![]()
Análogamente, como el calor Q2 es sustraído también a volumen constante, y en tales condiciones que L4-1=0, podemos escribir:
![]()
y por ser el fluido un gas perfecto:
![]()
Por consiguiente, el rendimiento térmico ideal para el ciclo Otto teórico resulta:
he= (calor suministrado – calor sustraído)/ calor suministrado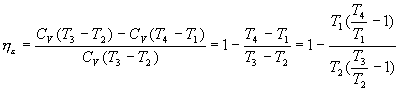
Para las transformaciones adiabáticas de compresión 1-2 y de expansión 3-4 obtenemos, respectivamente:
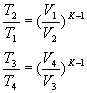
y como es V1=V4 y V2=V3, podemos escribir:
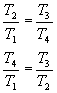
Introduciendo esta relación en la expresión del rendimiento he(así como la que existe entre las temperaturas T1 y T2 de la fase 1-2 de compresión adiabática), resulta:
![]()
Indicando con ![]() la relación entre los respectivos volúmenes V1 y V2 del principio y final de la carrera de compresión –a la cual llamaremos “relación volumétrica de compresión”-, se obtiene la expresión final del rendimiento térmico ideal del ciclo Otto.
la relación entre los respectivos volúmenes V1 y V2 del principio y final de la carrera de compresión –a la cual llamaremos “relación volumétrica de compresión”-, se obtiene la expresión final del rendimiento térmico ideal del ciclo Otto.
![]()
El rendimiento térmico del ciclo Otto es, por tanto, función de la relación de compresión y exponente k, relación de los calores específicos de fluido operante. Aumentando ![]() , aumente he; aumentando los valores de los calores específicos, disminuye k y, en consecuencia, también el rendimiento térmico he. Por ello, el ciclo ideal, para el cual k=1.4, tiene un rendimiento térmico superior al ciclo de aire, dado el caso que, para éste, posee k un valor medio más bajo, por variar los calores específicos con la temperatura.
, aumente he; aumentando los valores de los calores específicos, disminuye k y, en consecuencia, también el rendimiento térmico he. Por ello, el ciclo ideal, para el cual k=1.4, tiene un rendimiento térmico superior al ciclo de aire, dado el caso que, para éste, posee k un valor medio más bajo, por variar los calores específicos con la temperatura.


